Archivo etiqueta matemática
Conociendo coordenadas reales con Kinect
Hola!
En el marco del proyecto de SLAM que estamos desarrollando en este grupo de investigación (Ver aquí), les mostraré un extracto del trabajo en proceso.
Kinect nació como un periférico para la consola de juegos Xbox 360 de Microsoft. Llegaba dispuesto a cambiar la forma de jugar a los videojuegos, transformándonos en el «mando» con el que controlar a los personajes y demás movimientos virtuales, con movimientos corporales.
Rápidamente, dado su éxito, este dispositivo ha ampliado sus horizontes, convirtiéndose en un sistema de visión artificial muy utilizado por investigadores de todo el mundo, para lo cual la propia Microsoft decidió lanzar un SDK (software development kit) para facilitar el desarrollo de aplicaciones basados en Kinect.
Cuenta con una cámara RGB, un sensor de profundidad y un micrófono, que nos proporciona mucha información.
De las imágenes tomadas con la cámara RGB, podemos conocer las coordenadas “virtuales” de un punto (pixel) visible, como se muestra a continuación:

Además de estos datos, el Kinect nos otorga información sobre la profundidad de cada pixel (depth), gracias a su cámara infrarroja.
De esta manera, utilizando trigonometría, podemos calcular las coordenadas reales del punto reflejado en cada pixel.
Tomando como ejes cartesianos las rectas perpendiculares que pasan por el centro geométrico de la imagen, obtenemos las coordenadas virtuales en 2 dimesiones (Xo;Yo) del plano de la imagen.
Para esto, conociendo los ángulos de visión del Kinect y las medidas –en pixeles- de la imagen, podemos calcular a qué ángulo corresponde cada pixel.
El ángulo de cada pixel se calcula así: 57º/Width = xAngle; y 43º/Height = yAngle. Por lo que multiplicando por Xo e Yo respectivamente, obtenemos los ángulos en X e Y (desde el centro) del punto virtual, que coincidirá con los ángulos del punto real.
Una vez obtenidos estos ángulos, y conociendo la distancia real al punto en cuestión: Depth (proporcionada por el Kinect), calculamos las coordenadas del punto real.
Zr = Depth;
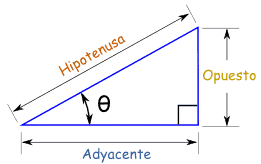
Estos valores se pueden obtener gracias a las razones trigonométricas que surgen de un triángulo rectángulo. En particular que: tan(«ángulo») = Opuesto / Adyacente
En nuestro caso, consideramos que la cámara (Kinect) se encuentra en el vértice correspondiente al ángulo «tita» (ángulo que ya hemos calculado), y también conocemos la distancia del lado “Adyacente” (Depth), por lo que la única incógnita por calcular es la distancia del lado “Opuesto”, que corresponderá a la distancia real de nuestro punto desde el centro de la imagen o visión de la cámara (coordenadas reales: Xr e Yr).
Xr = Tg(xAngle) x Depth;
Yr = Tg(yAngle) x Depth;
Robotics as a way of getting students closer to mathematical thinking
Today I’d like to share with you a fragment of «A Mathematician’s Lament», by Paul Lockhart.
So how do we teach our students to do mathematics? By choosing engaging and natural problems suitable to their tastes, personalities, and level of experience. By giving them time to make discoveries and formulate conjectures. By helping them to refine their arguments and creating an atmosphere of healthy and vibrant mathematical criticism. By being flexible and open to sudden changes in direction to which their curiosity may lead. In short, by having an honest intellectual relationship with our students and our subject.
I think this post’s title and the cited fragment speak by themselves.
You can read the full piece here.
De modo que ¿cómo deberíamos enseñar matemáticas a nuestros estudiantes? Escogiendo problemas naturales e interesantes, que vayan con sus gustos, personalidades y nivel de experiencia. Dándoles tiempo para hacer descubrimientos y formular conjeturas. Ayudándoles a refinar sus argumentos y creando una atmósfera de crítica matemática sana y saludable. Siendo flexibles y abiertos a cambios súbitos en la dirección a la que apunte su curiosidad. En resumen, manteniendo una relación intelectual honesta con nuestros estudiantes y las matemáticas.
Creo que el título de este post, en conjunto con el fragmento citado, hablan por sí solos.
Pueden leer la pieza entera acá
.